Within CSE 252B: Computer Vision II, I developed an end-to-end pipeline capable of estimating the fundamental matrix of 2 source images.

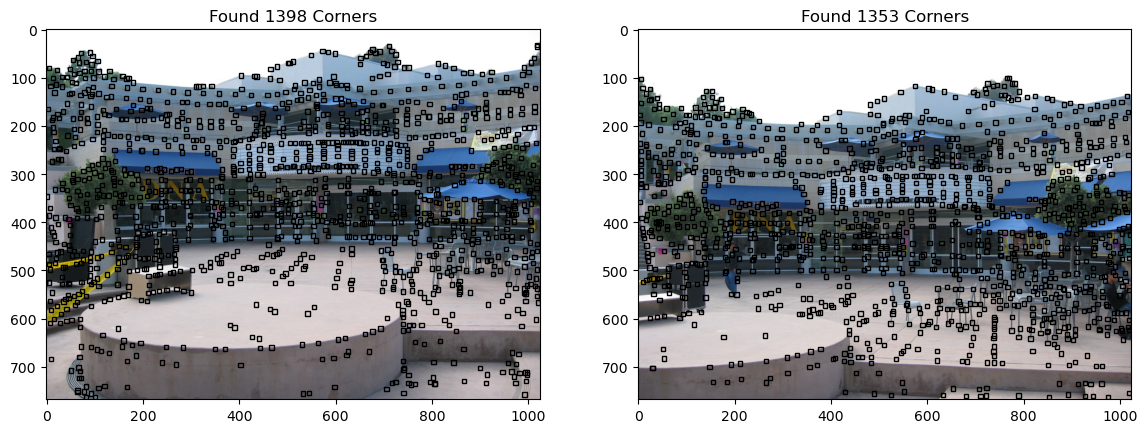
Feature Detection

Feature Detection was done by implementing the Shi-Tomsai Corner Detector with non-maximal suppression of the minor eigenvalue image, as well as the Forstner Point Operator for sub-pixel coordinates.

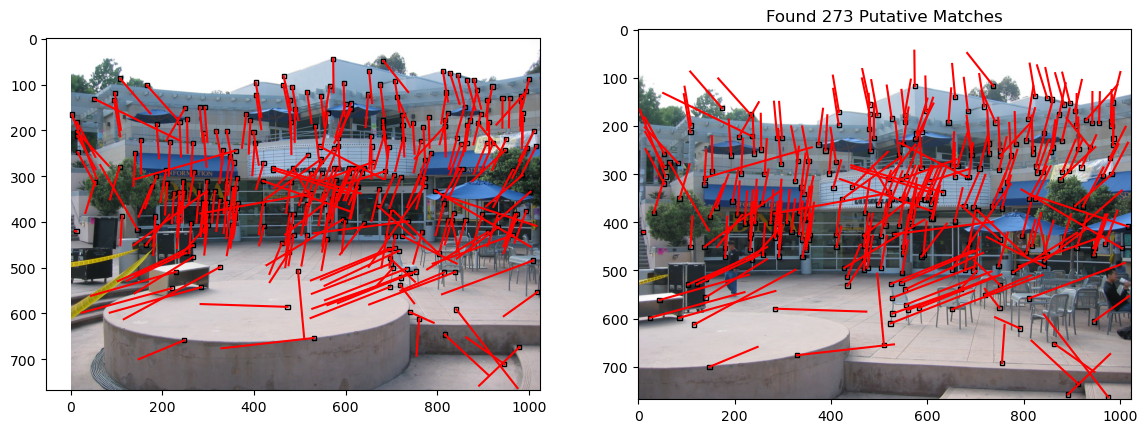
Feature Matching

Putative Feature Matching was accomplished by brute-force cross-correlation feature matching, filtering by correlation-coefficient thresholding, as well as correlation-coefficient uniqueness (relative to the 2nd highest correlation value). Bilinear interpolation was done due to account for sub-pixel feature coordinates.

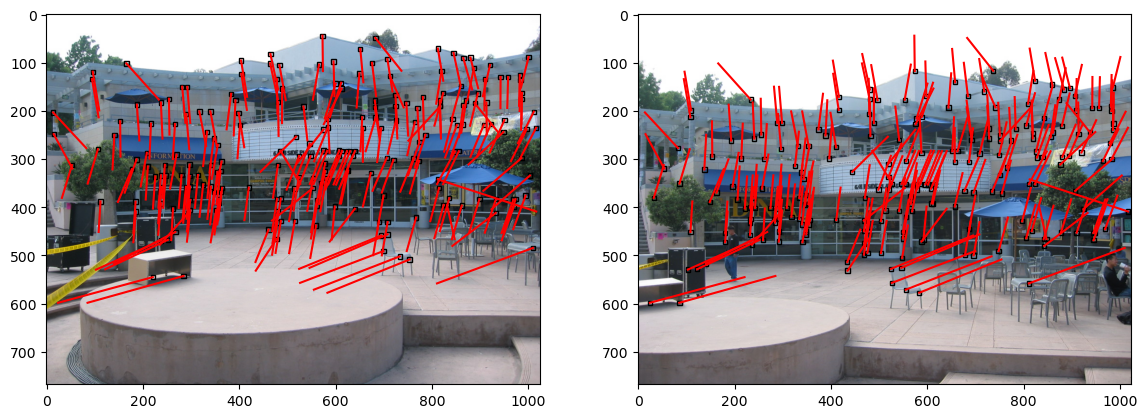
Outlier Rejection

Poor feature correspondences were removed by an implementation of the M-Estimator Sample Consensus (MSAC) algorithm. To estimate the Fundamental Matrix, the Seven-Point algorithm with Direct Linear Transform was used with Sampson Error.

Linear Estimate of the Fundamental MAtrix

Using the Direct Linear Transform Algorithm and all inlier point correspondences, the Fundamental Matrix was estimated.

Non-Linear Estimate of the Fundamental Matrix

Using two-view triangulation, the 2d point correspondences can be corrected (using the linear estimate of the Fundamental Matrix) and converted to 3d points. Then, by assuming canonical camera coordinates, a non-linear estimate of the second projection matrix can be computed.

To obtain the best estimate, the projection matrix was parameterized into an 11-dimensional space, optimized using the non-linear Levenberg-Marquardt Algorithm, and lastly unparameterized back as a 4x3 projection matrix.

Lastly, using the non-linear estimate of the Fundamental Matrix, the point-to-epipolar-line correspondences can be visualized using some salient features from the source image.